Notes on ReFT: Representation Finetuning

March 16, 2025

I've been investigating which fine-tuning methods are best for mitigating forgetting in language models during sequential skill learning. In doing so, I've come across many new fine-tuning and PEFT libraries, including a promising technique called ReFT. The paper mentions a 15x-65x improvement in parameter efficiency compared to LoRA, which caught my attention.

ReFT: Representation Finetuning for Language Models was written in May 2024 and accepted as a spotlight paper at NeurIPS later that year. The authors also released an accompanying library.

I recommend reading the paper, but I thought it'd be helpful to add my own notes on ReFT—how it works, where it comes from, and how you can use it. I'm assuming you know the basic Transformer architecture, and familiarity with other fine-tuning techniques like LoRA is helpful but not necessary.

Representations over weights

The core idea behind ReFT is that we should focus on representations, not weights.

What's a representation?

A representation $\mathbf{h} \in \mathbb{R}^d$ is simply the output at a particular token position after an intermediate layer. In the original ReFT paper, they focus on the Transformer architecture, so this is the output after a Transformer block (i.e. the MLP layer output + the residual stream).¹ For example, we start with our $n$ input tokens:

\mathbf{x} = (x_1, x_2, \dots, x_n)

Then we get our first set of representations after the embedding layer:

\mathbf{h}^{(0)} = (\mathbf{h}_1^{(0)}, \mathbf{h}_2^{(0)}, \dots, \mathbf{h}_n^{(0)})

And after passing through the $j$ th Transformer block, we get the $j$ th set of representations $\mathbf{h}^{(j)}$ .

Why focus on representations?

Let me (informally) break down what makes ReFT different:

When we modify weights, we modify the ways in which the model is doing computations
When we modify representations, we modify the actual intermediate results of computations

Models might not just use a single neuron to encode a concept. A single neuron might encode multiple concepts. If we focus on how we can modify representations, which encode concepts more naturally than the neuron values themselves, we might be able to fine-tune more effectively.

The recipe

Here's a high-level idea of how we can fine-tune a model with a focus on representations, rather than weights:

Take each intermediate representation $\mathbf{h}$ (outputs) at each token position for each layer.
Apply a function $\Phi$ to each representation to get a new representation $\Phi(\mathbf{h})$ .
Put those new representations back into the model.
During fine-tuning, learn the best $\Phi$ .

This general recipe isn't really new, by the way—adapter methods, which do just the above, have been around for some time. But ReFT differs from these adapter methods in a key way: it only applies $\Phi$ to certain tokens at certain layers. We'll get more into that later.

The question comes down to how we can parameterize $\Phi$ , or how exactly we should modify representations.

How to modify representations

There are many² different ways to modify intermediate representations, but the ReFT authors start from a particular method called distributed interchange interventions. Don't worry, it's not as scary as the name sounds—we'll work our way up to it, and here's a video walkthrough by Atticus Geiger (one of the ReFT/DII authors) and Neel Nanda if you want more detail.

You don't need to understand all of this to use ReFT—the goal of this section is just to derive $\Phi$ . So feel free to jump to the LoReFT equation below, but I think it's helpful to know where the equation comes from, and DIIs are a nice interpretability tool to have.

Causal abstractions

Let's say you have a big neural network, like GPT-4.5, and you're prompting it to add 3 numbers together to get a sum $S_2 = X+Y+Z$ . If you, a human, were to add 3 numbers together, maybe you'd do it in two steps:

$S_1 = X + Y$
$S_2 = S_1 + Z$

Is the neural network doing the same thing? How can we tell?

One way is to use a causal abstraction of the complex model:

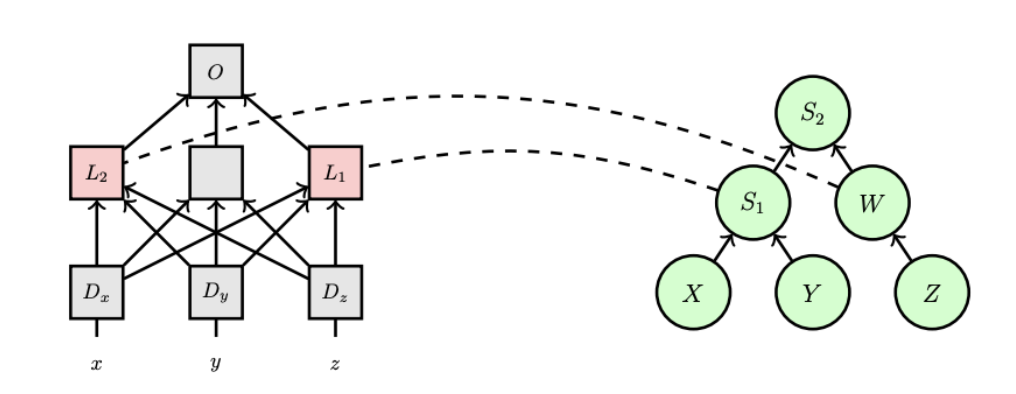causal model of addition and neural network Source: https://arxiv.org/pdf/2106.02997

On the left is part of the original neural network, and on the right is a causal abstraction. The (part of the) neural network takes in 3 representations of $X$ , $Y$ , and $Z$ as $D_x$ , $D_y$ , and $D_z$ .

A causal abstraction is just a small DAG that abstracts away part of the complex model. Our LLM isn't literally this DAG, but the intermediate steps we see in the DAG correspond to intermediate steps in the neural network. For example, the value of $S_1$ in the causal abstraction corresponds to some location $L_1$ in the neural network.

Isn't the graph a lot easier to look at than a big neural network? For one, it helps us know why or how the model makes certain decisions, and it might even allow us to modify the model in a desirable way.³

But while this abstraction is great, we don't know if it actually maps to what the LLM is really doing. Hopefully the real neural network is doing something equivalent, but we need a way to validate that mapping. We can do that with interchange interventions.

Interchange interventions

Let's say we've picked out some causal abstraction ahead of time, and we want to see if it actually maps to our neural network.

The setup:

We have a complex neural network $\mathcal{N}$
We have a simple causal abstraction $\mathcal{B}$
We have a hypothesis on which parts of $\mathcal{N}$ map to which parts of $\mathcal{B}$ , but we don't know if it's correct

We'll have $\mathcal{N}$ and $\mathcal{B}$ be the same neural network and causal model as in the figure above.

And our hypothesis:

The inputs $X$ , $Y$ , and $Z$ map to $D_x$ , $D_y$ , and $D_z$
The output $S_2$ maps to $O$
The intermediate value $S_1$ maps to $L_1$
The intermediate value $W$ maps to $L_2$

Now, if the neural network is doing a perfectly good job at computing the sum $S_2 = X+Y+Z$ , then we know that the inputs and outputs are mapped correctly (if they weren't mapped correctly, then we'd see unexpected outputs). So we'll just focus on making sure the intermediate values are mapped correctly.

We can test this by changing the intermediate neural network values in a clever way.

First, let's plug a base input into both models:

Base input: $X=1$ , $Y=1$ , $Z=1$ .
In the causal model, this means that $S_1=2$ and $W=1$ , so $S_2=3$ .
In the neural network, we should end up with an $O$ that also corresponds to $3$ .

Next, let's try a source input in both models:

Source input: $X=2$ , $Y=2$ , $Z=2$ .
In the causal model, this means that $S_1=4$ and $W=2$ , so $S_2=6$
We should also get $6$ for the neural network

What happens if we use the value of $S_1$ for the source input to replace the value of $S_1$ during the base input? Let's see what happens in the causal model:

For the source input, $S_1=4$ .
If we replace (or intervene) on $S_1$ for the base input, we add $W=1$ with $S_1=4$ to get $S_2=5$ .

In other words, we've replaced the intermediate step of $X+Y$ from the base input with the step from the source input. The trick here is that we can do the same thing with the neural network:

Compute $L_1$ (which we think maps to $S_1$ ) for the source input.
Start with the base input for the neural network, but replace $L_1$ with the value we got from the source input.
If $L_1$ truly maps to $S_1$ , then we should also get an output of $5$ .

If it turned out that $L_1$ didn't correspond to $S_1$ exactly, then we might see a different output. But that's okay, since we can just try a new mapping—maybe $L_2$ is what maps to $S_1$ instead.

To confirm that a mapping is correct, we can repeat the same process but with many more base inputs and source inputs. If we see consistent intermediate outputs, then we've found a good mapping.

The causal model mapping recipe

Start with a candidate mapping between $\mathcal{N}$ (the neural network) and $\mathcal{B}$ (the causal model).
Test that $L_i$ $L_{i}$ (locations in the neural network) and $S_i$ $S_{i}$ (nodes in the causal model) match up:
1. Get values for $L_i$ and $S_i$ with a source input.
2. Compute the outputs for $\mathcal{N}$ and $\mathcal{B}$ with the base input, but intervene on the values of $L_i$ and $S_i$ .
3. If the outputs are equal, then the mapping works for this base + source. Keep trying other base + source inputs until we're satisfied.
4. If the outputs aren't equal, then this mapping doesn't work.
Repeat the above with different $L_i$ and $S_i$ until we've mapped all intermediate steps of the causal model to the neural network.

Distributed interchange interventions

Now that we know what an interchange intervention is, what's a distributed interchange intervention?

There's a small problem with our recipe above—it'll throw away some perfectly good causal models. Here's an example of how:

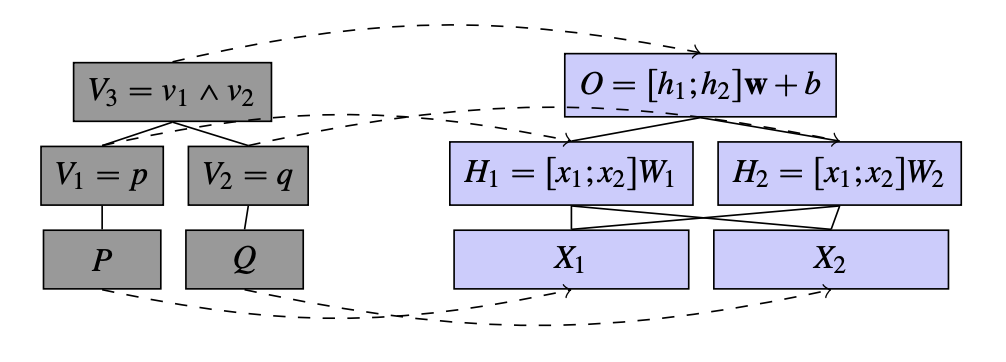causal model of boolean logic and neural net Source: https://arxiv.org/pdf/2303.02536

This is a neural network (on the right this time) that simply checks whether two boolean inputs $p$ and $q$ are both true, i.e. it outputs $p \wedge q$ .

Let's say that if our neural network outputs a value $O > 0$ , then this corresponds to $V_3$ being true (i.e. $p \wedge q$ is true), and that $O < 0$ corresponds to either $p$ or $q$ being false. We can use these params for the neural net:

$W_{1} = \begin{bmatrix}\cos(20^\circ) & -\sin(20^\circ)\end{bmatrix}$
$W_{2} = \begin{bmatrix}\sin(20^\circ) & \cos(20^\circ)\end{bmatrix}$
$\mathbf{w} = \begin{bmatrix}1 & 1\end{bmatrix}$
$b = -1.8$

For example, if we input [true, true] as $X_1=1$ , $X_2=1$ into the network, we get an output of $O = 0.08 > 0$ , which we interpret as true.

So can we map this causal model to the neural network? Try the following interchange intervention:

Base input: [false, true] or $X_1=0$ , $X_2=1$
Source input: [true, true] or $X_1=1$ , $X_2=1$
Intervene on $V_1$ or $H_1$

failed interchange intervention Source: https://arxiv.org/pdf/2303.02536

You'll see that while the causal model outputs true, the neural network outputs $O = -0.26 < 0$ , or false!

Normally we'd just throw this mapping and causal model away. But it's a bit surprising that such a simple problem can't be modeled so easily.

The DII authors found one small tweak to make this model work: if you rotate the representation $[H_1, H_2]$ by 20 degrees, you get a perfect causal abstraction! When I say "rotate", I mean do the following:

Compute your source input vector $\mathbf{s}$ and base input $\mathbf{h}$ .⁴ Since we're rotating the representations across multiple neurons, we set $\mathbf{h}$ equal to the vector $[H_1, H_2]$ (for the base input values).
Rotate $\mathbf{s}$ and $\mathbf{h}$ by some rotation matrix $\mathbf{R}$ .
Intervene on $\mathbf{h}$ with $\mathbf{s}$ in that rotated space.

So before, we were doing a normal intervention across the representations by replacing $\mathbf{h}$ with $\mathbf{s}$ . We could rewrite this as

\mathbf{h} + \mathbf{s} - \mathbf{h}

where we start with $\mathbf{h}$ , and intervene by adding $\mathbf{s}$ - $\mathbf{h}$ . When we intervene within a rotated space, we get a new representation:

\mathbf{h} + \mathbf{R}^\intercal(\mathbf{Rs} - \mathbf{Rh})

and when we try this on our example above, with a rotation of 20 degrees, we find that the mapping works.⁵

This is called distributed interchange intervention because we're now working in a rotated space across multiple, distributed neurons. As mentioned before, individual neurons might play multiple roles in representing multiple concepts, so rotating the neuron space helps us find that natural setting.

In most examples, we won't know what $\mathbf{R}$ should be ahead of time, so we do the following:

Constrain $\mathbf{R}$ to have orthonormal rows.
Learn $\mathbf{R}$ using gradient descent, based on how well the mapping matches up.⁶

So we can use the same recipe as in the previous section to find a causal mapping, except:

We use normal interchange interventions on the causal model.
We use distributed interchange interventions on the neural network, with gradient descent to learn $\mathbf{R}$ .

This process is called distributed alignment search. One advantage of using gradient descent and a distributed intervention here is that we are no longer using pure brute-force search to find a mapping.

From DIIs to ReFT

DIIs are useful because we have a way to modify a concept (or representation) in a neural network during computation. "Modify a concept" is a bit vague, so here's an example using our $X+Y+Z$ neural network from before:

The neural network computes $S_2 = X + Y + Z$ .
We can show (through distributed alignment search) that the neural network maps to a causal model. The causal model works in two steps:
1. $S_1 = X + Y$
2. $S_2 = S_1 + Z$
Now we have a mapping, and we know that the (distributed) location $L_1$ $L_{1}$ in the neural network corresponds to $S_1$ $S_{1}$ . If we want to modify the concept $S_1$ $S_{1}$ , we can use another DII to intervene on $L_1$ $L_{1}$ :
1. Use a source input $\mathbf{s}$ to compute a value for $L_1$ (in a rotated space defined by some $\mathbf{R}$ )
2. Use a base input $\mathbf{h}$ to compute the output $S_2$ , but replace the intermediate value(s) of $L_1$ with the one from the source input (also in the rotated space)

This final step, written mathematically, is just this:

\mathrm{DII}(\mathbf{h}, \mathbf{s}, \mathbf{R}) = \mathbf{h} + \mathbf{R}^\intercal(\mathbf{Rs} - \mathbf{Rh})

Where $\mathbf{R}$ is a matrix we've learned ahead of time, and we replace the old representation with the result of $\mathrm{DII}(\mathbf{h}, \mathbf{s}, \mathbf{R})$ . The key takeaway here is that the source input $\mathbf{s}$ controls how we modify the representation.

Stepping back, what was our original goal for this new fine-tuning method? We wanted to find an adapter function $\Phi$ that modifies the representations during fine-tuning in a precise way. What if we just used this as our adapter function, at various token and layer locations?

\Phi(\mathbf{h}, \mathbf{s}, \mathbf{R}) = \mathbf{h} + \mathbf{R}^\intercal(\mathbf{Rs} - \mathbf{Rh})

The problem is that now we don't know what $\mathbf{R}$ and $\mathbf{s}$ should be, since we aren't dealing with a particular causal graph. We can't specify them manually, so we need some way to determine their values.

We can deal with $\mathbf{R}$ in the same way as before—by making it a learnable parameter during fine-tuning.

Should we do the same with $\mathbf{s}$ ? If we learn it directly, i.e. just make it another parameter, then the value of $\mathbf{s}$ will be the same for every input $\mathbf{h}$ . Intuitively, we should probably intervene differently depending on the input, so maybe we can replace $\mathbf{s}$ with something like $\mathbf{Wh} + \mathbf{b}$ , where $\mathbf{W}$ and $\mathbf{b}$ are a learnable weight and bias. But since we also control $\mathbf{R}$ now, we can replace all of $\mathbf{Rs}$ with $\mathbf{Wh} + \mathbf{b}$ :⁷

\Phi_{\text{LoReFT}}(\mathbf{h}) = \mathbf{h} + \mathbf{R}^\top (\mathbf{W} \mathbf{h} + \mathbf{b} - \mathbf{R} \mathbf{h})

This is LoReFT—a particular low-rank parameterization of ReFT, with learnable params $\mathbf{R} \in \mathbb{R}^{r \times d}$ , $\mathbf{W} \in \mathbb{R}^{r \times d}$ , and $\mathbf{b} \in \mathbb{R}^{r}$ . Since this is low-rank, we have $r \ll d$ (a typical value of $r$ for a 7B model might be 4 or 8). And during fine-tuning, we're doing two things:

Learning the rotation $\mathbf{R}$ into the subspace
Learning the projected source $\mathbf{W} \mathbf{h} + \mathbf{b}$ (which is replacing $\mathbf{Rs}$ )

Like DII, we'll constrain $\mathbf{R}$ to have orthonormal rows.

We can also choose other parameterizations to get other variations of ReFT:

\Phi_{\text{DiReFT}}(\mathbf{h}) = \mathbf{h} + \mathbf{W}_2 (\mathbf{W}_1 \mathbf{h} + \mathbf{b})

In this variation, called DiReFT, we've made two changes from LoReFT:

Removed the part where we subtract $\mathbf{Rh}$
Replaced the rotation matrix $\mathbf{R}$ with a normal weight matrix $\mathbf{W}_2$ with no orthogonality constraints

Both of these changes help make training faster, at the cost of some accuracy. Note the similarity between this and LoRA, which applies a low-rank difference to weights, and DiReFT, which applies a low-rank difference directly to representations.

If you wanted to make your own ReFT variation, all you'd have to do would be to define:

The intervention function(s) $\Phi$
Where (at what layers/token positions) you want to apply your function(s)

We haven't addressed (2) yet—now that we know how to modify representations, how do we know which representations to modify?

Intervention locations

Before I dug through the ReFT paper in detail and wrote these notes, I started playing around with pyreft just to see what it could do. There were two things I noticed quickly:

I couldn't merge/fold the weights back into the model, like with LoRA.
I had to prepare my datasets in a particular way. That is, I had to specify intervention_locations (the exact token positions at which interventions occur) for my samples in my tokenized datasets.

As we've discussed before, we need to specify which layers and token positions to intervene at, or to apply $\Phi$ at. Since we only intervene at certain positions, we can't just merge the weights into the model—otherwise, we'd be modifying every single position.

Picking layers

This is more straightforward—we just need to decide which layers to do interventions at. The simplest answer is to choose all layers, and this works pretty well, but is the most expensive.

In the ReFT paper's experiments, they also try only intervening on certain layers. A common pattern is to skip every few layers, or every other layer.

Note that the intervention params we learn should be different for each layer.

With pyreft, you create interventions at every layer like this:

make_reft_intervention = lambda rank: LoreftIntervention(
    embed_dim=model.config.hidden_size,
    low_rank_dimension=rank
)
reft_config = ReftConfig(representations=[{
    "layer": layer,
    "component": "block_output",
    "low_rank_dimension": RANK,
    "intervention": make_reft_intervention(RANK)
} for layer in range(NUM_LAYERS)])
model = get_reft_model(model, reft_config)

As you can see, for each representation we need to specify:

The layer it's at
Which output it's applied to
The rank of $\mathbf{R}$ (for LoReFT)

Picking token positions

For a sample, intervention_locations refers to the token positions we're applying the interventions at. The easiest way create a dataset with an intervention_locations column is to use pyreft.make_last_position_supervised_data_module:

training_examples = [
    ["Who are you?", "🤖💬🌐🧠"],
    ["Who am I?", "👤❓🔍🌟"],
    ["What's 2+2? And provide some details?", "🔢➕🔢➡️🍀"],
    ["Why is the sky blue?", "🌍🛡️☀️➡️🔵🌌"],
    ["What's Apple's stock price? Estimated value is fine?", "🍏💹🤷‍♂️"],
]

data_module = pyreft.make_last_position_supervised_data_module(
    tokenizer,
    model,
    [prompt_no_input_template % e[0] for e in training_examples],
    [e[1] for e in training_examples],
    num_interventions=2,
)

The above snippet is taken from the official demo. Then when we view the intervention_locations, we can see that they'll be applied to the last (non-padding) token in each sample:

data_module['train_dataset']['intervention_locations']

[[[19], [19]], [[19], [19]], [[28], [28]], [[21], [21]], [[31], [31]]]

The outermost items in this list are just which sample we're at. So let's look at the first sample:

[[19], [19]]

For this sample, each item in this list is for a particular intervention. This is specified in ReftConfig, where you can see that the above example has NUM_LAYERS interventions. We can intervene at a particular layer, and (as explained later) we can also have multiple interventions per layer. So here, we might only have two interventions (say at layers 6 and 12).

Finally, the list [19] just says that we're intervening at token position 19 in this sample, which happens to be the last position. If we did [18, 19] instead, then this would be the last two positions.

Note that for each example, we decide whether to apply the intervention at each individual token position. But if we have a sequence of length $n$ , this gives $2^n$ possible choices for how to intervene. To simplify things, the authors stick to two hyperparameters:⁸

The number of prefix, or first positions $f$ to intervene on
The number of suffix, or last positions $l$ to intervene on

For example, if we set $f=3$ and $l=5$ , then we'll intervene on the first 3 tokens and the last 5 tokens. This helps during hyperparameter searches, since we only have to try a few different values of $f$ and $l$ .

We can do this using pyreft.make_multiple_position_supervised_data_module and setting the positions kwarg. Here is what $f=3$ and $l=5$ looks like:

data_module = pyreft.make_multiple_position_supervised_data_module(
    tokenizer,
    model,
    [prompt_no_input_template % e[0] for e in training_examples],
    [e[1] for e in training_examples],
    positions="f3+l5",
    num_interventions=2,
    nonstop=False,
    share_weights=True
)

data_module['train_dataset']['intervention_locations']

[[[0, 1, 2, 15, 16, 17, 18, 19], [0, 1, 2, 15, 16, 17, 18, 19]],
 [[0, 1, 2, 15, 16, 17, 18, 19], [0, 1, 2, 15, 16, 17, 18, 19]],
 [[0, 1, 2, 24, 25, 26, 27, 28], [0, 1, 2, 24, 25, 26, 27, 28]],
 [[0, 1, 2, 17, 18, 19, 20, 21], [0, 1, 2, 17, 18, 19, 20, 21]],
 [[0, 1, 2, 27, 28, 29, 30, 31], [0, 1, 2, 27, 28, 29, 30, 31]]]

As you can see, we're once again doing 2 interventions (for 2 different layers), but now we're intervening at multiple positions for each intervention. For the first example, we get positions 0-2 ( $f=3$ ) and 15-19 ( $l=5$ ).

Tied intervention weights

In the above example, you'll notice that the same weights are shared across all positions at the same layer. There is a parameter called share_weights in this helper function, so what happens if we set it to false?

data_module = pyreft.make_multiple_position_supervised_data_module(
    tokenizer,
    model,
    [prompt_no_input_template % e[0] for e in training_examples],
    [e[1] for e in training_examples],
    positions="f3+l5",
    num_interventions=2,
    nonstop=False,
    share_weights=False
)

data_module['train_dataset']['intervention_locations']

[[[0, 1, 2, 20, 20], [15, 16, 17, 18, 19]],
 [[0, 1, 2, 20, 20], [15, 16, 17, 18, 19]],
 [[0, 1, 2, 29, 29], [24, 25, 26, 27, 28]],
 [[0, 1, 2, 22, 22], [17, 18, 19, 20, 21]],
 [[0, 1, 2, 32, 32], [27, 28, 29, 30, 31]]]

Some interesting stuff happened here:

We still only have 2 interventions per example (since num_interventions=2), but the positions are different for each intervention.
It looks like the first intervention has the first 3 positions, and the second intervention has the last 5 positions.
A small quirk of pyreft: there are some extra positions in the prefix positions list (e.g. 20 for the first example), but these are after the sample ends. I assume these are for padding/collation reasons.

So if we set share_weights=True, we use the same intervention for all positions at the same layer. If we set share_weights=False, we use different intervention weights for the prefix and suffix.

If we want to apply interventions at the same number of layers as before, we need to double the number of interventions by setting num_interventions=4, which doubles the parameter count:

[[[0, 1, 2, 20, 20], [0, 1, 2, 20, 20], [15, 16, 17, 18, 19], [15, 16, 17, 18, 19]],
 [[0, 1, 2, 20, 20], [0, 1, 2, 20, 20], [15, 16, 17, 18, 19], [15, 16, 17, 18, 19]],
 [[0, 1, 2, 29, 29], [0, 1, 2, 29, 29], [24, 25, 26, 27, 28], [24, 25, 26, 27, 28]],
 [[0, 1, 2, 22, 22], [0, 1, 2, 22, 22], [17, 18, 19, 20, 21], [17, 18, 19, 20, 21]],
 [[0, 1, 2, 32, 32], [0, 1, 2, 32, 32], [27, 28, 29, 30, 31], [27, 28, 29, 30, 31]]]

A small efficiency trick

If we're repeating the same prompt multiple times, one advantage of setting $f=0$ is that we can take advantage of a saved KV-cache. For example, if we have a long prompt like "You are a helpful assistant..." and we're only intervening on some of those tokens, the KV cache will always be the same for that prompt prefix, so we can use that cache and generate an answer with nearly zero overhead.

The unified PEFT framework, and why REFT doesn't fit

There's a nice paper that unifies different PEFT techniques. These are:

LoRA
Adapter tuning
Prefix tuning

The paper shows a more general formula for PEFT techniques, and how these 3 methods all fit into that formula.

ReFT doesn't really fit into this framework though (and this isn't necessarily a bad thing).⁹ ReFT applies interventions selectively to different token positions at different layers, and the PEFT framework only supports applying the same transformation at every position. If we think of the sequence/token position dimension as a time dimension, another way to say this is that the PEFT framework lacks a notion of time that ReFT requires.

Using pyreft

Here's the official demo if you're looking for how to use the pyreft library. After you've gone through that, below are some small tips for speedbumps I encountered.

Using pre-tokenized datasets

The provided helper functions are nice but I wanted to use some datasets I had already tokenized. Here's a helper function that returns the intervention locations for a tokenized example.

def get_intervention_locations(
    example,
    num_interventions,
    num_prefix_positions=0,
    num_suffix_positions=1,
    share_weights=True,
):
    prefix_start_location = 0
    suffix_end_location = len(example['input_ids']) - 1
    dummy_position = len(example['input_ids']) - 1

    if 0 in example['attention_mask']:
        first_zero_mask = example['attention_mask'].index(0)
        suffix_end_location = first_zero_mask - 1
        dummy_position = first_zero_mask

    prefix_end_location = min(prefix_start_location + num_prefix_positions - 1, suffix_end_location)
    suffix_start_location = max(suffix_end_location - num_suffix_positions + 1, prefix_start_location)

    if prefix_end_location > suffix_start_location:
        # If the prefixes and suffixes overlap, prioritize the prefixes (is this the best approach? should be fine for now since I'm tying weights)
        prefixes = range(prefix_start_location, prefix_end_location + 1)
        suffixes = range(prefix_end_location + 1, suffix_end_location + 1)
    else:
        prefixes = range(prefix_start_location, prefix_end_location + 1)
        suffixes = range(suffix_start_location, suffix_end_location + 1)

    prefixes = list(prefixes)
    suffixes = list(suffixes)

    if len(prefixes) < num_prefix_positions:
        prefixes.extend([dummy_position] * (num_prefix_positions - len(prefixes)))

    if len(suffixes) < num_suffix_positions:
        suffixes.extend([dummy_position] * (num_suffix_positions - len(suffixes)))

    if share_weights:
        intervention_locations = [prefixes + suffixes] * num_interventions
    else:
        intervention_locations = [prefixes, suffixes] * num_interventions

    return {"intervention_locations": intervention_locations}

Then I used it like this:

from functools import partial

NUM_POSITIONS = 11

my_dataset = my_dataset.map(partial(
    get_intervention_locations,
    num_interventions=NUM_LAYERS,
    num_prefix_positions=NUM_POSITIONS,
    num_suffix_positions=NUM_POSITIONS,
    share_weights=True
), batched=False, num_proc=16)

Evals

If you run into an error like AttributeError: 'CausalLMOutputWithPast' object has no attribute 'mean' when trying to include an eval set in your ReftTrainerForCausalLM, here's a quick patch that might help.

Choosing hyperparams

Here are the important new hyperparams¹⁰ that we discussed above:

The number of prefix positions to intervene on
The number of suffix positions to intervene on
Which layers to intervene on
Whether to tie intervention params across different positions in the same layer

For specific tips on how to tune these, I recommend looking at Appendix D.2 of the ReFT paper.

What's next?

As the authors have mentioned, the nice thing about ReFT is that it's a pretty general framework—you can design your own parameterizations like LoReFT or DiReFT, so there's a lot more work to be done in exploring architectures here. Again, please check out the original paper if you haven't already, and try out the library.

You could probably try to apply ReFT to other intermediate outputs in a Transformer model, e.g. after just the attention layers. But most interpretability work, e.g. on sparse autoencoders, focuses on these representations at the ends of each block. ↩
For example, using sparse autoencoders and modifying in feature space. ↩
For example, let's say your LLM is predicting professions based on age and gender. And maybe you don't want it to use gender as part of the computation. You could find the causal graph that has profession as an output, with age and gender as nodes, and then edit (or intervene on) the "gender" node to get less biased results. This paper does something similar, except they use circuits of SAE features instead. ↩
The original paper uses $\mathbf{b}$ for the hidden dimension, but I'm using $\mathbf{h}$ instead for consistency. ↩
In the DII paper, the complete definition of a DII is a bit more nuanced. We actually take the vector space we rotate into and decompose it into parts, so that we can intervene with multiple source inputs for all but one subspace (which keeps a base input). See Definition 3 in the paper for more detail. ↩
This is another detail we're glossing over a bit—we need an actual loss function if we want to do gradient descent. We can handle this by assuming that the neural network and causal model now output distributions over values, and not just single discrete values. Then we can make a differentiable loss function based on how similar those distributions are. ↩
I think one reason they do this is that $\mathbf{s}$ itself has a dimension of $d$ , whereas $\mathbf{Rs}$ has a dimension of $r$ . Learning $\mathbf{s}$ directly would require a large $\mathbf{W} \in \mathbb{R}^{d \times d}$ matrix, but directly learning $\mathbf{Rs}$ only needs a smaller $\mathbf{W} \in \mathbb{R}^{r \times d}$ . This also makes the final expression a little cleaner. ↩
The authors use $p$ and $s$ , but to avoid confusion with $\mathbf{s}$ I'm using $f$ and $l$ . ↩
I think the term "PEFT" is a little confusing here because it stands for "parameter-efficient fine-tuning". And ReFT is definitely a form of parameter-efficient fine-tuning. So when I'm saying it doesn't fit into the PEFT framework, I just mean that it can't be expressed under the same general formula that previous methods can be. ↩
"New" meaning different from older techniques like LoRA. ↩

bew.